example3_3 条间关联事件

说明

目的

    1. 学习如何处理相邻条的关联事件；
    1. 学习TCutG的用法；
    1. 利用TGraph fit拟合两参数关联关系；

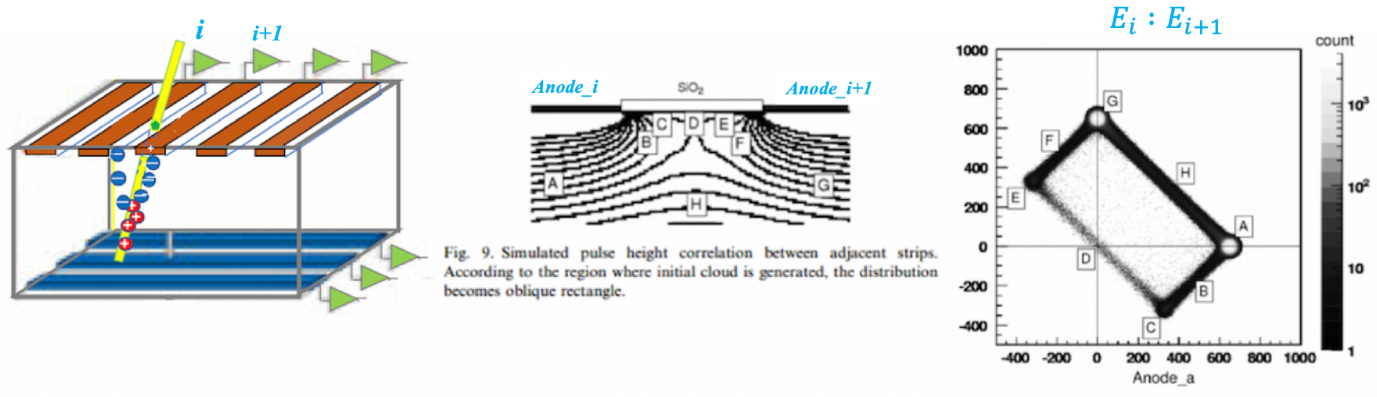
相邻条关联（cross-talk）

  • 入射粒子入射到两条之间的缝隙，载流子被相邻两条收集；

  • 某一条上有很大的能量沉积，导致相邻条产生感应信号；

  • 相邻条之间的信号关联关系与粒子的入射位置，以及入射深度都有关系，如下图(入射粒子沉积能量相同)所示；

    • 相邻条的关联在低能入射粒子（如alpha放射源），注入到浅层(BCDEF)时尤为复杂。如在BF位置，两侧产生的的脉冲信号一正一负；
    • 当入射粒子(高能)穿过DSSD时(AHG)两侧信号都是正的。

  • 一般情况下ADC只接受正脉冲信号,因此只能看见(AHG)范围内的关联，即$E = E_{i} + E_{i+1}$;

    avatar

数据

  • S4的Ring一侧，条宽很窄、条间距很小，因此相邻条之间具有显著的关联。
  • 在pie条中这种关联相对不明显

实验数据实际操作

打开s4dith.toot并继承tree结构

In [1]:
%jsroot on
In [2]:
TFile * ipf = new TFile("../s4dith.root","read");
TTree * tree = (TTree*)ipf->Get("tree");
TCanvas * c1= new TCanvas;





















Ring的第13条与相邻条的共享












In [3]:



    


tree->Draw("redith[14]:redith[13]>>h43a(800,0,1600,800,0,1600)","","colz");
c1->Draw();



    















    
































In [4]:



    


tree->Draw("redith[12]:redith[13]>>h23a(800,0,1600,800,0,1600)","","colz");
gPad->SetLogz();
c1->Draw();



    















    
































In [5]:



    


tree->Draw("redith[13]>>h1(800,0,1600)","redith[12]>0");
TH1F *h1=(TH1F*)gROOT->FindObject("h1");
tree->Draw("redith[13]>>h2(800,0,1600)","redith[14]>0");
h1->SetLineColor(kRed);
h1->Draw("same");
c1->Draw();



    















    


































说明


    

  • redith13,蓝色能谱是连续的，故13条和14条之间能量分配是随机的;
    • 

  • redith13,红色能谱有峰结构，故 13条与12条之间，13条有全能量沉积;
    • 
















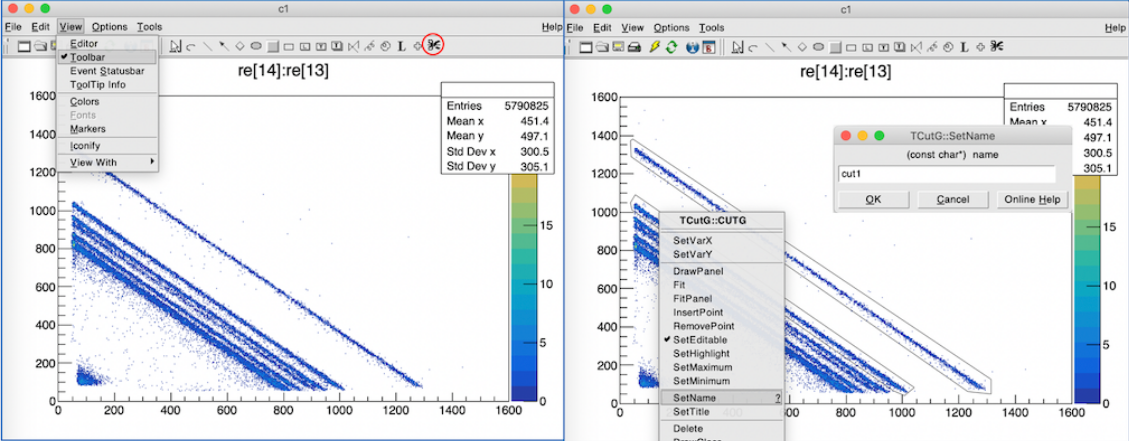
TCutG - 选择图形中的封闭区域作为Cut条件
手动Cut操作方法


    

  • 画tree的二维关联图
    • 

  • 选择Edit->Toolbar
    • 

  • 在下面出现的图形选项中选择最后一项 ✂️
    • 

  • 连续点击鼠标左键选择闭合区域，双击结束
    • 

  • 点击鼠标右键，选择SetName改名称；不改的话缺省为CUTG
    

    avatar
    

    • 



将Cut结果存储成root文件（代码方法）


TFile *fout=new TFile("out.root","recreate"); //创建文件
cut1->Write();//写入cut1
cut2->Write();//写入cut2



存成文件（代码方法）


root [0] cut1->SaveAs("cut1.C")
Info in <TCutG::SaveAs>: C++ Macro file: cut1.C has been generated



加载已存储好的cut1.C文件（代码方法）


root [1] gROOT->Macro("cut1.C"); //等价于 .x cut1.C
Info in <TCanvas::MakeDefCanvas>:  created default TCanvas with name c1



特别注意：


在


tree->Draw("re:pe");



图中选在区域存成的cut.C文件，其座标轴变量为


cutg->SetVarX("pe");
cutg->SetVarY("re");



因此，该文件在别的图中使用时，不起作用。


tree->Draw("re[10]:pe[10]","cut");//cut不会起作用



因此，需要修改相应的变量名称：



c+
cutg->SetVarX("pe[10]");
 cutg->SetVarY("re[10]");


才能使用。


代码内使用TCutG


//载入TCutG
gROOT->Macro("cut1.C");//gROOT->ProcessLine(".x cut1.C");
//获得TCutG的pointer "cut1"为SetName时指定的name
TCutG *cutg1 = (TCutG *)gROOT->GetListOfSpecials()->FindObject("cut1");
TCutG *cutg2 = (TCutG *)gROOT->GetListOfSpecials()->FindObject("cut2");
...

//判断点(x,y)是否在TCutG以内，    
bool bcut=cutg1->IsInside(Double_t x,Double_t y);//1-is inside, 0- not inside
if(bcut) {
 ...
}
















cut并查看cut.C文件
    

  • cut1.C: 对应alpha谱中  8.6931  MeV
    • 

  • cut2.C: 对应alpha谱中  6.6708  MeV
    • 














In [6]:



    


!cat cut1.C cut2.C



    















    






{
//========= Macro generated from object: CUTG/Graph
//========= by ROOT version6.16/00
   
   TCutG *cutg = new TCutG("CUTG",6);
   cutg->SetVarX("redith[13]");
   cutg->SetVarY("redith[14]");
   cutg->SetTitle("Graph");
   cutg->SetFillStyle(1000);
   cutg->SetPoint(0,52.3462,1369.43);
   cutg->SetPoint(1,36.7049,1304.84);
   cutg->SetPoint(2,1269.24,69.1066);
   cutg->SetPoint(3,1306.78,79.8708);
   cutg->SetPoint(4,640.459,770.936);
   cutg->SetPoint(5,52.3462,1369.43);
   cutg->Draw("");
}
{
//========= Macro generated from object: CUTG/Graph
//========= by ROOT version6.16/00
   
   cutg = new TCutG("CUTG",6);
   cutg->SetVarX("redith[13]");
   cutg->SetVarY("redith[14]");
   cutg->SetTitle("Graph");
   cutg->SetFillStyle(1000);
   cutg->SetPoint(0,48.1752,1070.18);
   cutg->SetPoint(1,39.8331,1018.51);
   cutg->SetPoint(2,1003.34,47.578);
   cutg->SetPoint(3,1026.28,71.2594);
   cutg->SetPoint(4,500.73,603.014);
   cutg->SetPoint(5,48.1752,1070.18);
   cutg->Draw("");
}






















载入多个TCutG文件
    

  • 由于root在加载TCutG对象时，默认命名为cutg，所以多次载入TCutG文件会因为重名而报错；
    • 

  • 正确的做法是将多个TCutG文件合并为一个并作适当修改;
    

    合并
    

    • 














In [7]:



    


!rm allcut.C
!cat cut1.C>>allcut.C
!cat cut2.C>>allcut.C
!cat allcut.C



    















    






{
//========= Macro generated from object: CUTG/Graph
//========= by ROOT version6.16/00
   
   TCutG *cutg = new TCutG("CUTG",6);
   cutg->SetVarX("redith[13]");
   cutg->SetVarY("redith[14]");
   cutg->SetTitle("Graph");
   cutg->SetFillStyle(1000);
   cutg->SetPoint(0,52.3462,1369.43);
   cutg->SetPoint(1,36.7049,1304.84);
   cutg->SetPoint(2,1269.24,69.1066);
   cutg->SetPoint(3,1306.78,79.8708);
   cutg->SetPoint(4,640.459,770.936);
   cutg->SetPoint(5,52.3462,1369.43);
   cutg->Draw("");
}
{
//========= Macro generated from object: CUTG/Graph
//========= by ROOT version6.16/00
   
   cutg = new TCutG("CUTG",6);
   cutg->SetVarX("redith[13]");
   cutg->SetVarY("redith[14]");
   cutg->SetTitle("Graph");
   cutg->SetFillStyle(1000);
   cutg->SetPoint(0,48.1752,1070.18);
   cutg->SetPoint(1,39.8331,1018.51);
   cutg->SetPoint(2,1003.34,47.578);
   cutg->SetPoint(3,1026.28,71.2594);
   cutg->SetPoint(4,500.73,603.014);
   cutg->SetPoint(5,48.1752,1070.18);
   cutg->Draw("");
}






















修改后













In [8]:



    


!cat allcut1.C



    















    






{
//========= Macro generated from object: CUTG/Graph
//========= by ROOT version6.16/00
   
   TCutG *cutg = new TCutG("cut1",6);//*****修改cut的名字*****
   cutg->SetVarX("redith[13]");
   cutg->SetVarY("redith[14]");
   cutg->SetTitle("Graph");
   cutg->SetFillStyle(1000);
   cutg->SetPoint(0,52.3462,1369.43);
   cutg->SetPoint(1,36.7049,1304.84);
   cutg->SetPoint(2,1269.24,69.1066);
   cutg->SetPoint(3,1306.78,79.8708);
   cutg->SetPoint(4,640.459,770.936);
   cutg->SetPoint(5,52.3462,1369.43);
   //cutg->Draw("");*****注释此行*****
//}*****注释此行*****
//{*****注释此行*****
//========= Macro generated from object: CUTG/Graph
//========= by ROOT version6.16/00
   
   cutg = new TCutG("cut2",6);//*****修改cut的名字*****
   cutg->SetVarX("redith[13]");
   cutg->SetVarY("redith[14]");
   cutg->SetTitle("Graph");
   cutg->SetFillStyle(1000);
   cutg->SetPoint(0,48.1752,1070.18);
   cutg->SetPoint(1,39.8331,1018.51);
   cutg->SetPoint(2,1003.34,47.578);
   cutg->SetPoint(3,1026.28,71.2594);
   cutg->SetPoint(4,500.73,603.014);
   cutg->SetPoint(5,48.1752,1070.18);
  // cutg->Draw("");*****注释此行*****
}




















In [9]:



    


gROOT->Macro("allcut1.C");
c1->Clear();
tree->Draw("redith[14]:redith[13]>>(800,0,1600,800,0,1600)","cut2","colz");
c1->Draw();



    















    
































In [10]:



    


tree->Draw("redith[14]:redith[13]>>h2(800,0,1600,800,0,1600)","cut1","colz");
c1->Draw();



    















    


































相邻条修正公式
$x$条能量-道址x的关系：$$e_{x} = k_{x}x + b_{x}$$
$y$条能量-道址x的关系：$$e_{y} = k_{y}y + b_{y}$$
$x$条和$y$条能量和：$$e = e_{x} + e_{y} = k_{x}x + k_{y}y + b_{x} + b_{y}$$
$x$条和$y$条能量关联：$$y = kx + b$$
以上二式联立有：$$k = - \frac{k_{x}}{k_{y}}$$
$$b = \frac{e - b_{x} - b_{y}}{k_{y}}$$


    

  • 从相邻的关联（y-x)拟合得到斜率$k$和截距$b$;
    • 

  • 由两个能量值($E_{1}, E_{2}$)对应的($b_{1}, b_{2}$)，可得$k_{y}$和($b_{x} + b_{y}$)；
    • 

  • 从$k$得到$k_{x}$；
    • 

  • 需要其他约束才能分别确定$b_{x}$和$ b_{y}$;
    • 














In [11]:



    


TGraph * gr;
TF1 * fp1;



    













In [12]:



    


// fill selected tree data to a graph,
// refers to https://root.cern.ch/root/roottalk/roottalk03/0638.html
gr = new TGraph(tree->GetSelectedRows(),tree->GetV2(), tree->GetV1());
gr->Draw("p");//draw point
c1->Draw();



    















    


































拟合得到$k, b$
    

  • 下面为利用cut1条件的拟合
    • 














In [13]:



    


fp1= new TF1("fp1","pol1",0,1600);
fp1->SetLineColor(kRed);
gr->Fit(fp1);
fp1->Draw();
h2->Draw("same colz");
c1->Draw();



    















    























    






****************************************
Minimizer is Linear
Chi2                      =       230910
NDf                       =         4679
p0                        =      1377.13   +/-   0.198913    
p1                        =     -1.01342   +/-   0.000255772 



















In [14]:



    


Double_t p0;
Double_t p1;
TString stree;



    













In [15]:



    


p0=fp1->GetParameter(0);
p1=fp1->GetParameter(1);
stree.Form("redith[14]:-%f*redith[13]+redith[14]>>hre2(800,0,1600,800,0,1600)",p1);
tree->Draw(stree.Data(),"redith[13]>0&&redith[14]>0","colz");
c1->Draw();



    















    


































相邻条能量之和












In [16]:



    


TH1F *hre=(TH1F*)hre2->ProjectionX();
hre->SetName("hre");
TH1F *h13=new TH1F("h13","h13",800,0,1600);
TH1F *h14=new TH1F("h14","h14",800,0,1600);
tree->Draw("redith[13]>>h13");
tree->Draw("redith[14]>>h14");
h13->SetLineColor(kGreen);
h14->SetLineColor(kBlue);
hre->SetLineColor(kRed);



    













In [17]:



    


hre->Draw();
h13->Draw("same");
h14->Draw("same");
c1->Draw();



    















    


































    

  • 利用cut1和cut2下相邻条关联图，计算刻度系数，计算事件的能量:  $e = e_{x} + e_{y} = k_{x}x + k_{y}y + b_{x} + b_{y}$
    • 
















在判断相邻条相加后事件所属的位置时
    

  • 直接指定为能量更大的一侧的位置
    • 

  • 也可以按照能量权重计算更精确的位置
$$x_{w} = \frac{e_{1}x_{1} + e_{2}x_{2}}{e_{1} + e_{2}}$$
    • 














In [18]:



    


!jupyter nbconvert example3_3.ipynb --to html



    















    






[NbConvertApp] Converting notebook example3_3.ipynb to html

[NbConvertApp] Writing 575083 bytes to example3_3.html




















In [ ]: